克鲁斯卡尔算法(Kruskal's algorithm)是两个经典的最小生成树算法的较为简单理解的一个。这里面充分体现了贪心算法的精髓。大致的流程能够用一个图来表示。这里的图的选择借用了Wikipedia上的那个。很清晰且直观。
首先第一步,我们有一张图,有若干点和边
例如以下图所看到的:
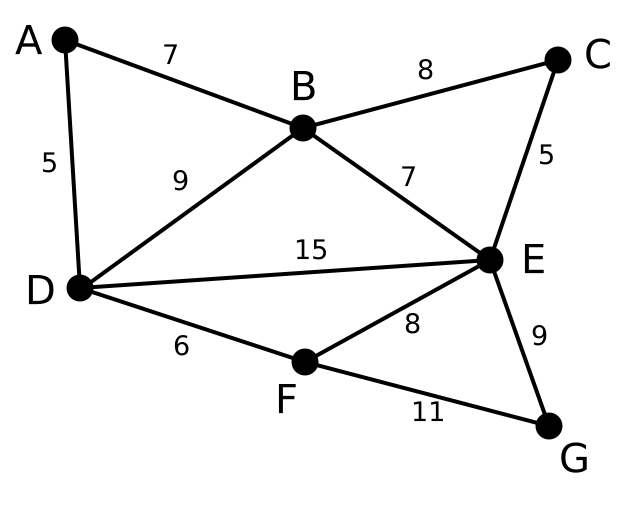
第一步我们要做的事情就是将全部的边的长度排序,用排序的结果作为我们选择边的根据。这里再次体现了贪心算法的思想。资源排序,对局部最优的资源进行选择。
排序完毕后,我们领先选择了边AD。 这样我们的图就变成了
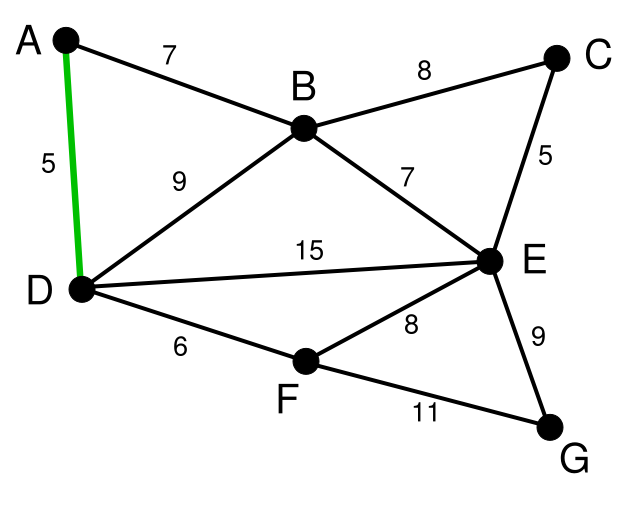
第二步,在剩下的变中寻找。我们找到了CE。这里边的权重也是5
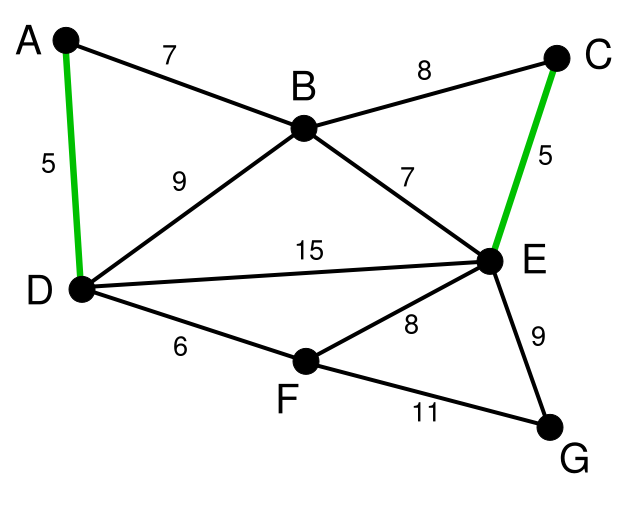
依次类推我们找到了6,7,7。完毕之后,图变成了这个样子。
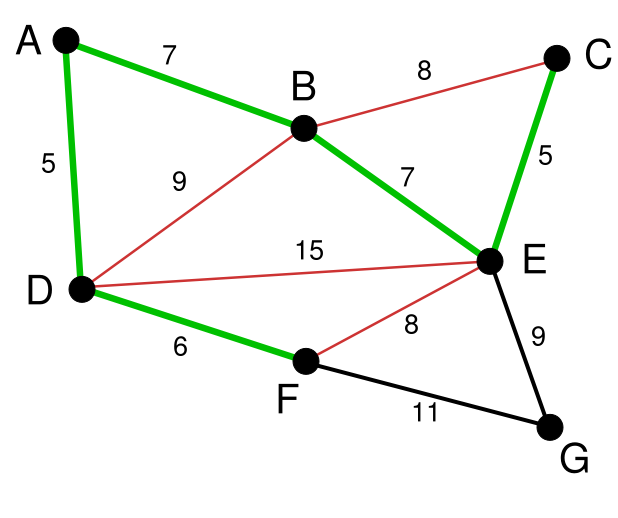
下一步就是关键了。以下选择那条边呢? BC或者EF吗?都不是,虽然如今长度为8的边是最小的未选择的边。可是如今他们已经连通了(对于BC能够通过CE,EB来连接,相似的EF能够通过EB, BA, AD, DF来接连)。所以我们不须要选择他们。相似的BD也已经连通了(这里的连通线用红色表示了)。所以最后就剩下EG和FG了。当然我们选择了EG。 最后成功的图就是下图:
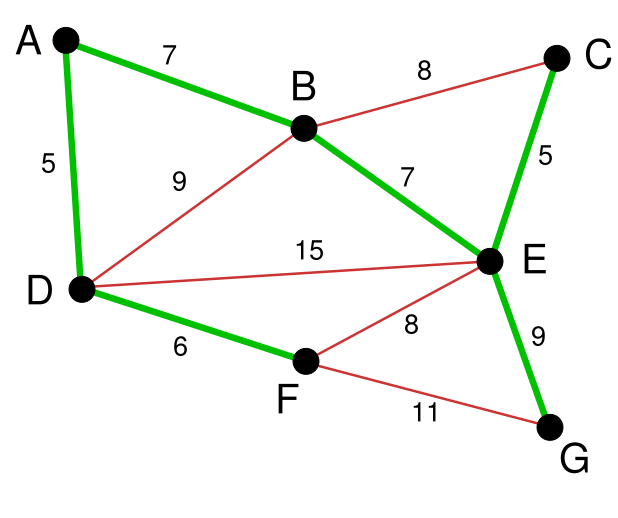
到这里全部的边点都已经连通了,一个最小生成树构建完毕。
假设要简要得描写叙述这个算法的话就是,首先边的权重排序。(从小到大)循环的推断是否须要选择这里的边。推断的根据则是边的两个顶点是否已经连通,假设连通则继续下一条。不连通就选择使其连通。这个流程还是很清晰明了。
可是在实现的时候,困难的地方在于怎样描写叙述2个点已然连通? 这里用到了并查集做辅助,至于并查集能够到去看看。
这里贴出并查集的代码和Kruscal的C++实现:
/* * * Disjoint_Set_Forest.h -- an implementation for disjoint set data structure * * Created by Ge Chunyuan on 04/09/2009. * * version: 0.1 */ #pragma once #ifndef _DISJOINT_SET_H_ #define _DISJOINT_SET_H_ #include <vector> template <typename T> class DisjointSet { public: DisjointSet(); ~DisjointSet(); void makeSet ( const std::vector<T>& s ); bool findSet ( const T& s, T& parent); void Union ( const T& s1, const T& s2 ); protected: struct Node { int rank; T data; Node* parent; }; int m_nElementCnt; int m_nSetCnt; std::vector<Node*> m_Nodes; }; template< class T> DisjointSet<T>::DisjointSet() { m_nElementCnt = 0; m_nSetCnt = 0; } template< class T> DisjointSet<T>::~DisjointSet() { for (int i=0;i<m_nElementCnt;i++) delete m_Nodes[i]; } template< class T> void DisjointSet<T>::makeSet( const std::vector<T>& s ) { m_nElementCnt += (int)s.size(); m_nSetCnt += (int)s.size(); std::vector<T>::const_iterator it = s.begin(); for (;it != s.end(); ++ it) { Node* pNode = new Node; pNode->data = *it; pNode->parent = NULL; pNode->rank = 0; m_Nodes.push_back(pNode); } } template< class T> bool DisjointSet<T>::findSet( const T& s, T& parent) { Node* curNode = NULL; bool find =false; for (int i=0;i<(int)m_Nodes.size();i++) { curNode = m_Nodes[i]; if (curNode->data == s) { find = true; break; } } if (!find) return false; // find the root Node* pRoot = curNode; while (pRoot->parent != NULL) { pRoot = pRoot->parent; } // update all curNode's parent to root while (curNode != pRoot) { Node* pNext = curNode->parent; curNode->parent = pRoot; curNode = pNext; } parent = pRoot->data; return true; } template< class T> void DisjointSet<T>::Union( const T& s1, const T& s2 ) { Node* pNode1 = NULL; Node* pNode2 = NULL; int find = 0; for (int i=0;i<(int)m_Nodes.size();++i) { if (m_Nodes[i]->data == s1 || m_Nodes[i]->data == s2 ) { find ++; if (m_Nodes[i]->data == s1) pNode1 = m_Nodes[i]; else pNode2 = m_Nodes[i]; } } // not found if ( find != 2) return ; if (pNode1->rank > pNode2->rank) pNode2->parent = pNode1; else if (pNode1->rank < pNode2->rank) pNode1->parent = pNode2; else { pNode2->parent = pNode1; ++ pNode1->rank; } --m_nSetCnt; } #endif //_DISJOINT_SET_H_
// Kruscal_Algorithm.cpp : Defines the entry point for the console application. // #include "stdafx.h" #include <string> #include <vector> #include <algorithm> #include <iostream> #include "Disjoint_Set_Forest.h" struct Vertex { Vertex () { } Vertex (std::string n) { name = n; } bool operator==(const Vertex& rhs) { return name == rhs.name; } bool operator!=(const Vertex& rhs) { return name != rhs.name; } std::string name; }; struct Edge { Edge () {} Edge (Vertex v1, Vertex v2, int w) { this->v1 = v1; this->v2 = v2; this->w = w; } Vertex v1; Vertex v2; int w; }; struct EdgeSort { bool operator()(const Edge& e1, const Edge& e2) { return e1.w<e2.w; } }; struct PrintEdge { void operator() (Edge e) { std::cout<< "edge start from "<<e.v1.name <<" to "<<e.v2.name << " with length = "<<e.w <<std::endl;; } }; class Graph { public: void appendVertex ( const Vertex& v1) { m_vertexs.push_back(v1); } void appendEdge ( const Vertex& v1, const Vertex& v2, int w) { m_edges.push_back( Edge(v1,v2,w) ); } void minimumSpanningKruskal () { std::vector<Edge> result; std::sort (m_edges.begin(), m_edges.end(), EdgeSort()); DisjointSet<Vertex> dv; dv.makeSet(m_vertexs); std::vector<Edge>::iterator it = m_edges.begin(); for (;it!= m_edges.end();++it) { Vertex p1; Vertex p2; bool b1 = dv.findSet(it->v1, p1 ); bool b2 = dv.findSet(it->v2, p2 ); if ( b1&& b2 && (p1 != p2)) { dv.Union(p1, p2); result.push_back(*it); } } for_each(result.begin(), result.end(), PrintEdge()); } protected: std::vector<Vertex> m_vertexs; std::vector<Edge> m_edges; }; int _tmain(int argc, _TCHAR* argv[]) { Graph gr; Vertex a("A"); Vertex b("B"); Vertex c("C"); Vertex d("D"); Vertex e("E"); Vertex f("F"); Vertex g("G"); gr.appendVertex(a); gr.appendVertex(b); gr.appendVertex(c); gr.appendVertex(d); gr.appendVertex(e); gr.appendVertex(f); gr.appendVertex(g); gr.appendEdge(a,b,7); gr.appendEdge(a,d,5); gr.appendEdge(b,c,8); gr.appendEdge(b,d,9); gr.appendEdge(b,e,7); gr.appendEdge(c,e,5); gr.appendEdge(d,e,15); gr.appendEdge(d,f,6); gr.appendEdge(e,f,8); gr.appendEdge(e,g,9); gr.appendEdge(f,g,11); gr.minimumSpanningKruskal(); system("pause"); return 0; }